polinômios
Um polinômio qualquer pode ser representado pela expressão:
a0 xn + a1 xn – 1 + a2 xn -2 + ... + an – 1 x + an
A função polinomial será definida por:
P(x) = a0xn + a1xn – 1 + a2xn -2 + ... + an – 1x + an
Com:
a0 , a1 , a2, … , an – 1 e an são números complexos e n ![]() N.
N.
• Valor numérico de um polinômio
Se observarmos um polinômio qualquer P(x) = 5x4 – 3x3 + x2 – x + 2, para acharmos o seu valor numérico que é o valor de P(x), temos que ter um valor para a incógnita x.
Então, se dissermos que x = 2 o valor que encontrarmos para P(2) quando substituirmos x por 2 será o valor numérico do polinômio.
P(2) = 5 . 24 – 3 . 23 + 22 – 2 + 2
P(2) = 5 . 16 – 3 . 8 + 4 – 2 + 2
P(2) = 80 – 24 + 4
P(2) = 56 + 4
P(2) = 60
Concluímos que o valor numérico do polinômio P(x) = 5x4 – 3x3 + x2 – x + 2, quando
x = 2 será P(2) = 60.
• Raiz ou zero do polinômio
Se pegarmos um polinômio qualquer P(x) = - 2x3 + 5x2 – x + 1 = 0, a raiz dele será um número qualquer b se, somente se, o valor numérico do polinômio for zero quando
x = b.
Exemplo:
P(x) = x2 - 1, para calcularmos o zero da função, devemos colocar P(x) = 0, então:
x2 - 1 = 0
x2 = 1
x = + 1 ou - 1
Concluímos que -1 e +1 é raiz do polinômio P(x) = x2 - 1.
• Grau de um polinômio
Um polinômio é formado por vários monômios separados por operações, então o grau de um polinômio corresponde ao monômio de maior grau. O único polinômio que não possui grau é o polinômio nulo P(x) = 0, por exemplo:
• P(x) = x3 - x2 + 2x -3 → temos 3 monômios que possuem grau, o que tem maior grau é x3, então o polinômio tem o mesmo grau que ele.
P(x) = x3 - x2 + 2x -3 é do 3º grau.
• P(x) = 5x0 = 5 → grau zero.
Quando trabalhamos com divisão, utilizamos também a multiplicação no processo. Observe o seguinte esquema:

Vamos dividir um polinômio por um monômio, com o intuito de entendermos o processo operatório. Observe:
Exemplo 1:

Caso queira verificar se a divisão está correta, basta multiplicar o quociente pelo divisor, com vistas a obter o dividendo como resultado.
Verificando → quociente * divisor + resto = dividendo
4x * (3x² + x – 2) + 0
12x³ + 4x² – 8x
Caso isso ocorra, a divisão está correta. No exemplo a seguir, iremos dividir polinômio por polinômio. Veja:
Exemplo 2:

Verificando → quociente * divisor + resto = dividendo
(2x – 5) * (5x – 9) + (–5)
10x² – 18x – 25x + 45 + (–5)
10x² – 43x + 45 – 5
10x² – 43x + 40
Observe o exemplo de número 3:

Verificando → quociente * divisor + resto = dividendo
(3x² + x – 1) * (2x² – 4x + 5) + 0
6x4 – 12x³ + 15x² + 2x³ – 4x² + 5x – 2x² + 4x – 5
6x4 – 10x³ + 9x² + 9x – 5
Exemplo 4:
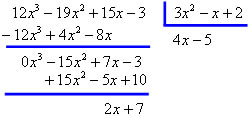
Verificando → quociente * divisor + resto = dividendo
(4x – 5) * (3x² – x + 2) + (2x + 7)
12x³ – 4x² + 8x – 15x² + 5x – 10 + (2x + 7)
12x³ – 19x² + 13x – 10 + 2x + 7
12x³ – 19x² + 15x – 3
